So far we used sigmoid function as the activation function in the hidden layer. I am going to try other functions also such as, hyperbolic tangent and rectified linear unit (ReLU). Firstly we look into hyperbolic tangent. The definition of hyperbolic tangent function and its derivative is as follow.
ここまで、隠れ層の活性化関数にはシグモイド関数を使って来た。ここでその他の関数、 双曲正接関数やrectified linear unit (ReLU) 等も使ってみようと思う。まず双曲正接関数についてみていく。双曲正接関数の定義と微分は以下のようになる。
ここまで、隠れ層の活性化関数にはシグモイド関数を使って来た。ここでその他の関数、 双曲正接関数やrectified linear unit (ReLU) 等も使ってみようと思う。まず双曲正接関数についてみていく。双曲正接関数の定義と微分は以下のようになる。
$$\begin{align*}\tanh(x) &= \frac {exp(x) - \exp(-x)} {exp(x) + exp(-x)} \\ \\ \frac{d}{dx}\tanh(x) &= 1-\tanh^2(x) \end{align*}$$
Hyperbolic tangent function is a linear transformation of sigmoid function and their relationship can be derived as follow.
双曲正接関数はシグモイド関数を線形変換したものになっており、その関係は以下のように導出できる。
$$\begin{align*} \tanh(x) &= \frac {exp(x) - exp(-x)} {exp(x) + exp(-x)} \\ \\ &= \frac{1 - exp(-2x)}{1 + exp(-2x)} \\ \\ &= \frac{1+exp(-2x)-2exp(-2x)}{1 + exp(-2x)} \\ &= 1 - \frac{2exp(-2x)}{1+exp(-2x)} \\ \\ &= 1 -2(\frac{1+exp(-2x)-1}{1+exp(-2x)})\\ \\ &= 1 -2 (1 - \frac{1}{1+exp(-2x)}) \\ \\ &= 1 -2 (1 - \sigma(2x)) \\ \\ &= 2\sigma(2x) -1 \end{align*}$$
双曲正接関数はシグモイド関数を線形変換したものになっており、その関係は以下のように導出できる。
where $\sigma(x)=\frac{1}{1+exp(x)}$ is sigmoid function.
ここで、$\sigma(x)=\frac{1}{1+exp(x)}$はシシグモイド関数
ここで、$\sigma(x)=\frac{1}{1+exp(x)}$はシシグモイド関数
As $tanh$ has greater gradient than sigmoid function, applying $tanh$ should fasten the network optimisation. Also, the range of output of $tanh$ is $[-1, 1]$ and this is better suited for optimisation. The reason is described in "Efficient Backprop" by Le Cunn et al. Simply said, when all the components of an input vector have the same sign (plus or minus), then the weight vector of an activation unit is updated in either all decreased or all increased at the same time. Therefor, in order a weight vector to get optimised to have weight values with both positive and negative values, the network has to repeat the iteration more. This slows down the optimisation.
$tanh$ はシグモイド関数よりも急な勾配を持っているので、ネットワークの最適化がより高速になる。また、$tanh$の出力の値域が $[-1, 1]$ であり、"Efficient Backprop" by Le Cunn et al で述べられる理由により、ネットワークの最適化促進に一役買うことになる。簡単に言うと、レイヤーへの入力が全て同じ符号(正・負)を持っていたとすると、ある活性化ユニットの重みベクトルが更新される際には全ての重みの値が同時に増えるか、全ての重みの値が同時に減る、のどちらかにしかならない。これによって、重みが正負両方の値を持つ最適値に収束するためにはネットワークは最適化を何度も繰り返すことになり、全体の最適化が遅くなるのである。
$tanh$ はシグモイド関数よりも急な勾配を持っているので、ネットワークの最適化がより高速になる。また、$tanh$の出力の値域が $[-1, 1]$ であり、"Efficient Backprop" by Le Cunn et al で述べられる理由により、ネットワークの最適化促進に一役買うことになる。簡単に言うと、レイヤーへの入力が全て同じ符号(正・負)を持っていたとすると、ある活性化ユニットの重みベクトルが更新される際には全ての重みの値が同時に増えるか、全ての重みの値が同時に減る、のどちらかにしかならない。これによって、重みが正負両方の値を持つ最適値に収束するためにはネットワークは最適化を何度も繰り返すことになり、全体の最適化が遅くなるのである。
Code (Modified Part)
from numpy import tanh ### Forward pass # Output from the hidden layer x_out = tanh(B1+np.dot(W1, x_hid)) # Output from the output layer y_out = softmax(B2+np.dot(W2, x_out)) ### Backward pass t = t.reshape((-1, 1)) # Output layer error = y_out - t dEdW2 += np.dot(error, x_out.T) / n_train dEdB2 += error / n_train # Hidden layer error = np.dot(W2.T, error) * (1-x_out*x_out) dEdW1 += np.dot(error, x_hid.T) / n_train dEdB1 += error / n_train
Result
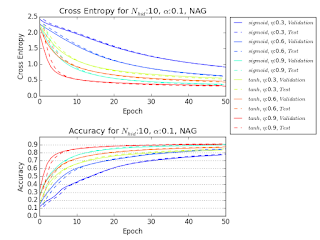
Following figures illustrates the effect of $tanh$ activation function compared against sigmoid function. The experiment is conducted using 10 mini-batch updates and Nesterov's accelerated gradient. The optimisation is accelerated effectively.
以下の表は活性化関数を $tanh$ にした時のネットワークの変化を、シグモイド関数の場合と比較して示している。実験には10分割のミニバッチ更新と Nesterov's accelerated gradient を用いた。最適化が促進されているのが分かる。
以下の表は活性化関数を $tanh$ にした時のネットワークの変化を、シグモイド関数の場合と比較して示している。実験には10分割のミニバッチ更新と Nesterov's accelerated gradient を用いた。最適化が促進されているのが分かる。