Rectified Linear Unit (ReLU) is computationally cheap and can avoid vanishing gradient problem in back-propagation, so it is widely used in deep learning. Following is the definition and the derivative of ReLU.
Rectified Linear Unit (ReLU) は計算量が少なく、vanishing gradient problem を回避できるのでディープラーニングでよく使われる。以下がその定義とその導関数である。
$$\begin{align*} f(x) &= max(0, x) \\ \\ \frac{df(x)}{dx} &= (sign(x)+1)/2 \end{align*}$$
Rectified Linear Unit (ReLU) は計算量が少なく、vanishing gradient problem を回避できるのでディープラーニングでよく使われる。以下がその定義とその導関数である。
Unlike sigmoid or hyperbolic tangent function, the derivatives of ReLU do not converge to $0$ at $x\rightarrow\inf$, so network is optimised faster, and the error is propagated properly to the next layer even for networks with multiple hidden layers. However, if a unit is not activated, then the parameters of the unit are not updated. Their update values are always $0$. So depending on the configuration of optimisation parameters, it is possible that network does not converge to its optimal weight. The following illustration shows it. In addition to it, it is also possible that a unit is never activated during training, the presence of such dead unit leads to the decrease of network's representation capacity.
ReLU をシグモイドや双曲正接関数と比較した場合の最大の特徴は、導関数の値が $x\rightarrow\inf$ でも $0$ にならないことである。これによって、学習の速度が速くなること、また、多層ネットワークでは伝搬されて来たエラーをそのまま次のレイヤーに伝搬するので、階層の深いレイヤーでもパラメーターがきちんと更新されるという点である。ただし、活性化しなかったユニットのパラメーター更新量は $0$ になるので、更新パラメーター次第では最適値に収束しない場合がある。下図はそれを模式的に表している。また、重みの状態次第では訓練中に一度も活性状態にならないユニットが出現する。このような死亡状態のユニットが出現すると、それはすなわち隠れユニットの数が減少することに等しく、ネットワークの表現能力が下がってしまう。
ReLU をシグモイドや双曲正接関数と比較した場合の最大の特徴は、導関数の値が $x\rightarrow\inf$ でも $0$ にならないことである。これによって、学習の速度が速くなること、また、多層ネットワークでは伝搬されて来たエラーをそのまま次のレイヤーに伝搬するので、階層の深いレイヤーでもパラメーターがきちんと更新されるという点である。ただし、活性化しなかったユニットのパラメーター更新量は $0$ になるので、更新パラメーター次第では最適値に収束しない場合がある。下図はそれを模式的に表している。また、重みの状態次第では訓練中に一度も活性状態にならないユニットが出現する。このような死亡状態のユニットが出現すると、それはすなわち隠れユニットの数が減少することに等しく、ネットワークの表現能力が下がってしまう。
Code: ReLU
# ReLU function and its derivative
def ReL(x):
return np.maximum(0, x)
def dReL(x):
return (np.sign(x)+1) / 2
### Forward pass
# Output from the hidden layer
x_out = ReL(B1+np.dot(W1, x_hid))
# Output from the output layer
y_out = softmax(B2+np.dot(W2, x_out))
### Backward pass
t = t.reshape((-1, 1))
# Output layer
error = y_out - t
dEdW2 += np.dot(error, x_out.T) / n_train
dEdB2 += error / n_train
# Hidden layer
error = np.dot(W2.T, error) * dReL(B1+np.dot(W1, x_hid))
dEdW1 += np.dot(error, x_hid.T) / n_train
dEdB1 += error / n_train
Result
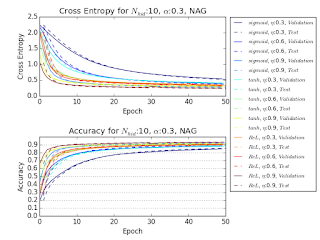
The following figures are the comparison of sigmoid function, hyperbolic tangent function, and ReLU as activation function. When learning rate and momentum are high, the network suffers from unstable improvement.
以下の図は活性化関数にシグモイド関数、双曲正接関数、ReLU を用いたときの最適化の様子を比較したものである。学習率とモーメンタムの値が高いところでは、改善性が不安定になる。
以下の図は活性化関数にシグモイド関数、双曲正接関数、ReLU を用いたときの最適化の様子を比較したものである。学習率とモーメンタムの値が高いところでは、改善性が不安定になる。
The following figures show the ratio of active units (units which were activated at least once during each of training/validation/test stage) throughout the iteration. When learning rate and momentum are high, many activation units are dead at the beginning of the optimisation.
以下の図は最適化途中の有効な活性化ユニット(訓練、バリデーション、テストのそれぞれの段階で最低一度は活性化したユニット)の割合を示している。学習率とモーメンタムの値が高いところでは、活性化ユニットの多くが初期段階で死亡してしまっている。
以下の図は最適化途中の有効な活性化ユニット(訓練、バリデーション、テストのそれぞれの段階で最低一度は活性化したユニット)の割合を示している。学習率とモーメンタムの値が高いところでは、活性化ユニットの多くが初期段階で死亡してしまっている。